Esercizi su interferenza della luce

Tag

Esercizi interferenza luce

Esperimento di Young: La luce attraversa una doppia fenditura e forma una figura di interferenza su uno schermo.

Lunghezza d’onda della luce visibile: da 400 nm a 750 nm.
1 nanometro = 10^-9 metri; 1 micrometro = 10^-6 m

Interferenza costruttiva, frange luminose:

a senθ = n * λ ; (n = 0; +- 1; +-2; +-3…)

Interferenza distruttiva, frange scure;

a senθ = (n – 1/2) * λ; (n = 0; +- 1; +-2; +-3…);

senθ = tanθ; se l’angolo è piccolo; senθ = Y / L.

1. In un esperimento di Young la figura di interferenza di due fenditure separate da una distanza a = 3,5 x 10^-3 mm, si forma su uno schermo posto a distanza L = 2,00 m. La luce monocromatica usata ha una lunghezza d’onda λ = 470 nm.
   a) Determina la distanza fra le prime due frange laterali (scure) e il massimo centrale.
   b) Calcola la distanza fra le prime due frange luminose simmetriche ai lati del massimo centrale, se il rapporto L/d triplica.
   c) Calcola la distanza fra le prime due frange luminose se l’esperimento viene condotto in acqua e la luce si propaga quindi in acqua dalle fenditure fino allo schermo.

C’è un massimo centrale sullo schermo a distanza L dalla metà distanza a fra le due fenditure dove c’è l’interferenza costruttiva. Poi di lato al massimo centrale ci sono due zone buie, sopra e sotto il massimo centrale, dove c’è interferenza distruttiva.

Y = distanza verticale sullo schermo dal centro del massimo centrale, fino al centro della frangia considerata.
L distanza dello schermo.
Y/L = tanα circa uguale a senα; λ = lunghezza d’onda

a Y / L = (n + 1/2) λ; interferenza distruttiva ( frange buie sullo schermo per  valori di n).

n = 0 ; prima frangia scura.

Y = 1/2 λ * L / a

Y = 1/2 * 470 * 10^-9 * 2 / (3,5 * 10^-6 m) = 0,134 m

Distanza fra le due frange scure = 2 Y

2Y = 0,134 * 2 = 0,269 m = 26,9 cm

Interferenza costruttiva: frange luminose

a Y / L = n * λ;

Se triplica L / a = 3 * ( 2 / 3,5 * 10^-6 = = 3 * 5,714 * 10^5 = 1,714 * 10^6

Y = λ * L / a = 470 * 10^-9 * 1,714 * 10^6 = 0,806 m

2 Y = 2 * 0,806 = 1,61 m

Se mettiamo l’acqua, la lunghezza d’onda diminuisce, perché diminuisce la velocità della luce. indice di rifrazione dell’acqua = 1,33
Velocità e lunghezza d’onda sono direttamente proporzionali perché V = λ x f; f è la frequenza della luce, è costante in ogni mezzo di propagazione.
Velocità in acqua = C / 1,33 = 3 * 10^8 / 1,33 = 2,26 * 10^8 m/s
λ’ = nuova lunghezza d’onda in acqua

facciamo una proporzione:

V = λ’ = C : λ
V : λ’ = C : 470 * 10^-9
λ’ = (V / C ) * 470 * 10^-9 = 0,752 * 470 * 10^-9 = 3,53 * 10^-7 m ( nuova lunghezza d’onda in acqua).

Y = 3,53 * 10^-7 * 2 / 3,5 * 10^-6 = 0,202 m (distanza della prima frangia luminosa dal max centrale).

2 Y = 0,404 m = 40,4 cm; (distanza fra le prime due frange luminose).

I percorsi non sono paralleli, ma si fa una approssimazione in quanto lo schermo è molto distante rispetto alla distanza d fra le fenditure.

d senθ = n * λ ; (n = 0; +- 1; +-2; +-3…)

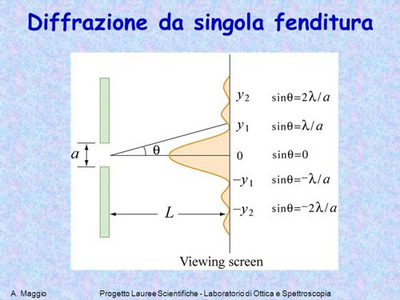
2)  Diffrazione della luce attraverso una fenditura

Trovare l’ampiezza della fenditura attraverso la quale un raggio di luce monocromatico di frequenza 5,3 • 10^14 Hz genera una prima banda scura spostata di 4,00•10^-3 gradi sullo schermo, rispetto alla posizione centrale.

La differenza di cammino delle onde secondarie generate dal bordo superiore della fenditura e dal suo punto medio è pari a:
a/2 sinθ.

a è la larghezza della fenditura.
Se questa differenza di cammino è pari a mezza lunghezza d’onda, λ/2, si avrà interferenza distruttiva delle due onde. Ci vuole λ.

C = λ x f; C = 3 x 10^8 m/s; velocità della luce.

λ = 3 x 10^8 / ( 5,3 x 10^14) = 5,66 x 10^-7 m

a/2 sinθ = m λ/2

a sin θ = mλ; per m = 1 si ha la prima banda scura.

a = λ / sinθ = 5,66 x 10^-7 / sin(4,00 x 10^-3° ) = 8,1 x 10^-3 m = 8,1 mm

2 bis Esercizio:

La larghezza di una fenditura è 2,0⋅10^-5 m.
Una luce che ha una lunghezza d’onda di 480 nm attraversa la fenditura e va a incidere su uno schermo posto a 0,50 m dalla fenditura.
Calcola la larghezza della frangia chiara più vicina alla frangia chiara centrale nella figura di diffrazione che si forma sullo schermo.
Soluzione = [0,012 m]

Diffrazione attraverso una fenditura larga a = 2 * 10^-5 m;

interferenza distruttiva se:

a * sen(θ) = n λ, si formano le frange  scure fra le frange chiare;

sen(θ) = Y /L; 

Y = distanza verticale sullo schermo del centro della frangia scura dal centro della frangia chiara centrale

Prima frangia scura:

a * sen(θ) = 1 * λ;

a * Y1/L = λ;

Y1 = λ * L / a;

Seconda frangia scura:

a * Y2/L = 2 * λ;

Y2 = 2 * λ * L / a;

Distanza frale due frange scure: (è la larghezza della frangia chiara fra le due scure).

Y2 – Y1 = (2 * λ * L / a) – (λ * L / a) ;

Y2 – Y1 = λ * L / a ;

Y2 – Y1 = 480 * 10^-9 * 0,50 / (2 * 10^-5) = 0,012 m;

Y2 – Y1 = 12 mm.

3) Reticolo di diffrazione

Un raggio di luce di lunghezza d’onda di 610 nm è inviato su un reticolo di diffrazione largo 1,40 cm e su cui sono praticate 5600 fenditure. 

– A quale angolo, rispetto alla perpendicolare al reticolo, si trova la terza frangia luminosa di diffrazione?

Si forma una figura di interferenza.

Distanza fra le fenditure:

d = 1,40 / 5600 = 2,5 * 10^-4 cm = 2,5 * 10^-6 m, (2,5 micrometri).

Massimi:

d sen(angolo) = m * lambda; m = 0, +-1, +-2, +- 3,…

lambda = 610 * 10^-9 m.

sen(angolo) = 3 lambda / d;

sen(angolo) = 3 * 610 * 10^-9 / (2,5 * 10^-6) = 0,732;

angolo = sen^-1(0,732) = 47° (angolo di diffrazione del 3° massimo).