Potenziale elettrico – Differenza di potenziale – Esercizi

Tag

potenziale - differenza di potenziale-esercizi

Il potenziale V  in un punto P del campo elettrico E è l’energia potenziale in quel punto per unità di carica.  

U = energia potenziale di due cariche a distanza r; U = k Q q / r ;

V = U/q si misura in   J/C, l’unità di misura del potenziale  si chiama V (volt). 

La differenza di potenziale ΔV (o d.d.p., o tensione ) VA – VB  tra due punti del campo, è il  lavoro che la forza compie per unità di carica;

è in pratica il lavoro del campo elettrico E.  U e V sono scalari. (U si misura in Joule; V in J/C = Volt).

      V =  U/q = k Q q / (r * q);    (si semplifica q);        
   
allora    V = k Q /r        ;  

VA – VB  = ( UA – UB) /q;

Lavoro L = Forza * Spostamento;

F = E * q; E = F / q;

 

  L = (VA – VA) * q  ; VA – VB  = (F/q) *  S =  E * S   ;

la differenza di potenziale VA – VB  è il lavoro del campo E.

Esercizio su Differenza di Potenziale 1)

Soluzione:
V = Somma algebrica di (k q/r);

r1 = a = 3,0 m; distanza di q da A

r2 = distanza di Q da A, si trova con Pitagora.

r2 = radice(a^2 + b^2) = radice(3,0^2 + 4,0^2) = 5,0 m;

VA = k q/r1 + k Q/r2;

VA = k * (+2,0 * 10^-9) /3,0 + k * (-2,0 * 10^-9 /5,0);

VA = 9* 10^9 * 10^-9 * ( 2/3 – 2/5) = 9 * 0,267 = + 2,4 V.

q dista 5,0 m da B;  Q dista a = 2,0 m da B.

VB = k * (+2,0 * 10^-9) /5,0 + k * (-2,0 * 10^-9 /3,0);

VB = 9 * 10^9 * 10^-9 * (2/5 – 2/3) = 9 * (- 0,267) = – 2,4 V;

VA – VB = + 2,4 – (- 2,4) = + 4,8 V.

Esercizio 2)

Consideriamo un pianeta dove l’accelerazione gravitazionale è la stessa della Terra, ma c’è anche un campo elettrico uniforme e parallelo a quello gravitazionale. Una palla di 1,40 kg e di carica 2,00 C è lanciata verso l’alto da un punto A a una velocità di 120 m/s e raggiunge B, il punto più alto della sua traiettoria, dopo un tempo t = 3,70 s.

Calcolare la differenza di potenziale tra i due punti A e B.

La forza è frenante, verso il basso; la forza risultante ferma la  carica q  ad altezza h;

F peso = m * g = 1,40 * (- 9,8) = – 13,72 N;

a = (v – vo) / t;

accelerazione  a = (0 – 120)/3,70 = – 32,43 m/s^2;

Troviamo l’altezza massima raggiunta  h:

h = 1/2 * a * t^2 +vo * t;

h = 1/2 * (- 32,43) * 3,70^2 + 120 * 3,70;

h = – 222 + 444 = + 222 m; (altezza massima raggiunta).

F risultante = m * a = 1,40 * (- 32,43) = – 45,41 N;

F risultante = m * g + q * E;

Forza elettrostatica; Fe = q * E;

Fe = – 45,41 – (-13,72) = – 31,68 N,

Campo elettrico:

E = Fe / q = – 31,68 / 2,00 = – 15,84 N/C;

Va – Vb  = (Lavoro della Forza elettrostatica) / (carica) = (Lavoro del campo E) / q;

(Il lavoro del campo elettrico è dato da  – DeltaV = V iniziale – V finale).

Va – Vb = (q * E) * h / q = E * h; lavoro del campo elettrico.

L /q = – 15,84 * 222 = – 3516 V = – 3,52 *10^3 V; il campo E frena la carica fa lavoro resistente.

Differenza di potenziale:

Delta V = Vb – Va = + 3,52 * 10^3 Volt.

Le cariche elettriche positive si spostano da un punto a potenziale maggiore verso un punto a potenziale minore.

VA > VB.

Nella realtà le cariche che si trasferiscono sono gli elettroni. Le cariche negative si muovono da potenziale minore verso il potenziale maggiore, (vanno dal – al +).

Per convenzione però si considera la corrente elettrica come un movimento di cariche positive che vanno dal + al – .

Esercizi su gravitazione; stelle binarie; stazione orbitante ISS – Problemi ambientali – Macchine – Satellite geostazionario – La cometa di Halley.

Tag

Problemi ambientali - macchine, Stazione orbitante - stelle binarie

Cygnus 61; moto intorno al centro di massa del sistema binario.

Soluzione proposta:

xCM = (MA xA + MB xB)/(MA +MB);

1 U A = 1,5 * 10^11 m; (distanza Terra Sole).

Poniamo xA = 0 UA;

xB = 84 UA;

xCM = 0,63  Ms * 84 / (0,63 + 0,70) = 39,79 UA; il centro di massa è più vicino ad A che é un po’ più massiccia della B.

xCM = 39,79 * (1,5 * 10^11 m) = 5,97 * 10^12 m; partendo da A;

RA = 5,97 * 10^12 m ; (distanza di A dal Centro di Massa CM);

RB = 84 UA – 39,79 UA = 44,21 UA = 6,63 * 10^12 m; (distanza di B dal CM).

La forza di attrazione fra le due stelle è la stessa; legge di gravitazione:

F = G * MA * MB / (R^2); 

R = 84 UA = 1,26 * 10^13 m; distanza fra le due stelle;

La forza è centripeta, verso il centro di massa;

Fcentripeta su A = MA * (omega)^2 * RA; (per la stella A, RA = 5,97 * 10^12 m);

Fcentripeta su B = MB* (omega)^2 * RB; (per la stella B);

Per la stella A:

G * MA * MB / (R^2) = MA * (omega)^2 * RA; (1);

MB = 0,63 * Msole = 0,63 *  2,0 * 10^30 = 1,26 * 10^30 kg;

ricaviamo omega^2; semplifichiamo MA

omega^2 = G MB /(R^2 * RA);

omega^2 = 6,67 * 10^-11 * (1,26 * 10^30) / [(1,26 * 10^13)^2 * 5,97 * 10^12 ];

omega^2 =  8,867 * 10^-20;

omega = radicequadrata( 8,867 * 10^-20) = 2,98 * 10^-10 rad/s;

omega = 2 pigreco / T;

T = 2 pigreco / omega = 6,28 / (2,98 * 10^-10 ) = 2,11 * 10^10 s;

T = periodo  in anni: 1 anno = 365 giorni * 24 h * 3600 s = 365 * 86400 s

T = 2,11 * 10^10 s  / (365 * 86400 s) = 669 anni circa. ( Periodo di rivoluzione intorno al centro di massa).

Esempio: Sirio A e Sirio B, un altro sistema binario:

Consideriamo il moto perfettamente circolare: Fcentripeta = m v^2 / R.

Moto circolare di Sirio A intorno al centro di massa:
mA = 2,14 masse solari = 2,14 * 2 * 10^30 = 4,28 *10^30 kg;
FA = mA * (a centripeta)  = mA * vA^2 / rA;  forza centripeta;
rA = 6,43 * 1,5 * 10^11 = 9,65 * 10^11 m;

(a centripeta) = vA^2 / rA = (3,85* 10^3)^2 / (6,43 * 1,5 * 10^11) = 1,537 * 10^-5 m/s^2
FA = m * a;
FA = 4,28 * 10^30  *  1,537 * 10^-5 = 6,58 * 10^25 N; Forza che Sirio B esercita su A;

Sirio A esercita la stessa forza su Sirio B;

FB = FA = F;
F = G * mA * mB / R^2; legge di gravitazione;

(rA + rB) = R distanza fra le due stelle;

mB = 1,03 masse solari = 1,03 * 2 * 10^30 = 2,06 * 10^30 kg;
Forza di attrazione fra le due stelle: (legge di Newton);

G * mA * mB / R^2 = 6,58 *10^25 N; legge di gravitazione;

G = 6,67 *10^-11 N * m^2 / kg^2;

R = radicequadrata[G * mA * mB/ (6,58 *10^25)]; 

R = radice(8,94 * 10^24) = 2,99 *10^12 m; distanza fra le due stelle A e B;

il centro di massa è più vicino a Sirio A che è più massiccia;

mA ed mB  girano intorno al centro di massa, mA a distanza rA, mB a distanza rB, più lontano dal centro di massa;

rA = 9,65 * 10^11 m;
rB = R – rA = 2,99 * 10^12 – 9,65 * 10^11;
rB = 2,03 * 10^12 m; (raggio dell’orbita di Sirio B);

mB * vB^2/rB = 6,58 * 10^25 N;

vB^2 = 6,58 * 10^25 * rB  / mB;
vB = radice quadrata[ 6,58 * 10^25 * 2,03 * 10^12 / (2,06 * 10^30)];

vB = radice(6,47 * 10^7) = 8044 m/s = 8,04 km/s; (velocità di SirioB).

2° esercizio:

Determinare il valore numerico della accelerazione di gravità g sulla
superficie della Terra e alla quota della stazione orbitante ISS. ( La stazione viaggia a una velocità media di 27600 km/h, completando 15,5 orbite al giorno e viene mantenuta in orbita ad una quota compresa tra 330 e 410 km. 

Legge di Gravitazione:

F = G * M terra * m / (Rterra)^2;

F = m * g = Forza peso.

g = G * M terra / (Rterra)^2; (sulla superficie terrestre, R = 6380 km =  6,38 * 10^6 m)

g = 6,67 * 10^-11 * 5,98 * 10^24 / (6,38 * 10^6)^2 = 9,799 m/s^2 = 9,8 m/s^2;

g è l’accelerazione di gravità.

h = 400 km circa dalla superficie, altezza della Stazione Internazionale.

R = 6,38 * 10^6 + 4 * 10^5 = 6,78 * 10^6 m;

g = G * M terra / R = 6,67 * 10^-11 * 5,98 * 10^24 / (6,78 * 10^6)^2;

g = 8,7 m/s^2; accelerazione di gravità sulla ISS.

Poiché la stazione gira intorno alla Terra questa accelerazione è centripeta, mantiene la stazione sull’orbita; chi è all’interno si trova in assenza di peso perché continuamente in caduta libera verso il centro della Terra. Si dice che in un sistema in rotazione esiste una forza centrifuga (forza inerziale, cioè apparente in un sistema in rotazione, sistema accelerato non inerziale) che annulla la forza centripeta.

3) Un satellite artificiale in orbita geostazionaria ruota intorno alla Terra restando sempre sopra lo stesso punto della superficie terreste. Sapendo che il raggio medio della terra è Rt=6,37 * 10^6 m e che il satellite si trova una quota di 36000 km sopra la superficie terrestre, trovare:

a. Quanto tempo impiega il satellite a compiere uno spostamento angolare di 60°;
b. La velocità e l’accelerazione centripeta del satellite;

Satellite geostazionario.

Un satellite geostazionario ha un periodo di 24 h (1 giorno), come il periodo di rotazione terrestre, in modo da rimanere sempre sullo stesso punto della superficie terrestre.

T = 24 h = 24 * 3600 s = 86400 s;

Rt=6,37 * 10^6 m;

h = 36 000 km = 36 000 000 m = 3,6 * 10^7 m;

Distanza dal centro della Terra, raggio dell’orbita:

R = Rt + h = 6,37 * 10^6 + 3,6 * 10^7 m = 4,24 * 10^7 m; ((circa 42 400 km).

omega = 2 pigreco / T = 6,28 / 86400 = 7,27 * 10^-5 rad/s; (velocità angolare);

alfa = omega * t;

alfa = 60° = pigreco/3 rad = 1,047 rad;;

t = alfa/ omega;

t = 1,047 /(7,27 * 10^-5) = 14404 s;

in ore:

t = 14404 / 3600 = 4 h; (1/6 del periodo);

essendo 60° =  1/6 dell’angolo giro, il satellite impiegherà 1/6 di 24 h.

v = omega * R = 7,27 * 10^-5 * 4,24 * 10^7;

v = 3082 m/s = 3,1 km/s (circa);

v = 3082 * 3,6 = 11100 km/h.

a centripeta = omega^2 * R ;

a = (7,27 * 10^-5)^2 * 4,24 * 10^7 = 0,22 m/s^2;

0,22 m/s^2 è il valore dell’accelerazione di gravità g se ci troviamo quella distanza R dalla Terra.

4) La cometa di Halley

Distanza media dal Sole: semiasse maggiore dell’ellisse.

r1 = distanza in afelio;  r2 = distanza in perielio;

r1 > r2

r medio:

r = (r1 + r2) / 2 = a  semiasse maggiore dell’ellisse

m v^2 / r = G M *m / r^2;

v^2 = G M / r;

v = 2 pigreco * r / T;

4 pigreco^2 *r^2 / T^2 = G M / r;

r^3 /T^2 = G M /(4 pigreco^2); 3a legge di Keplero;

r = radicecubica(G M T^2 / 39,478);

T = 75,8 anni = 75,8 * 365 giorni * 86400 s = 2,39 * 10^9 s;

r = radicecubica[6,67 * 10^-11 * 1,99 * 10^30 * (2,39 * 10^9)^2 / 39,478];

r = radicecubica[1,92 * 10^37] = 2,68 * 10^12 m;

(r = a = 2,68 * 10^12 m ;  semiasse maggiore dell’ellisse).

In UA: a = 2,68 * 10^12 / 1,5 * 10^11 = 17,9 UA.

in perielio:

r2 = 0,596 UA; r2 = 0,596 * 1,5 * 10^11 = 8,94 * 10^10 m;

v2 = 54,5 km/s = 54500 m/s; velocità in perielio.

r1 + r2 = 2 a;

r1 = 2a – r2 = 2 * 2,68 * 10^12 – 8,94 * 10^10;

r1 = 5,27 * 10^12 m; (distanza della cometa in afelio);

r1 = 5,27 * 10^12 / 1,5 * 10^11 = 35,1 UA; in afelio.

Si conserva il momento angolare; il momento della quantità di moto è costante perché il momento della forza M = r * F * sen(angolo), è nullo in quanto è una forza centrale che agisce lungo r e l’angolo fra  F ed r è 0.

r1 * m * v1 = r2 * m * v2;

velocità v1  in afelio:

v1 = r2 * v2 / r1 = 8,94 * 10^10 * 54,5 /(5,27 * 10^12);

v1 =  0,924 km/s = 924 m/s.

Quando la cometa è in afelio la sua velocità diminuisce, diventa minima, in perielio è massima.

Lavoro su automobili, mobilità, ambiente, qualità della vita, messaggi ingannevoli su libertà, natura, pressione delle auto sul pianeta di Teodoro Forcellini.

https://drive.google.com/file/d/1CVUL3yrr07fWD4IXhlEmvqLODuOsar_G/view

Pubblicità ingannevole?

Il dirigibile Hindenburg – Spinta di Archimede

Tag

dirigibile Spinta di Archimede

Il dirigibile Hindenburg, fabbricato in Germania nel 1936, è stato uno degli aeromobili più grandi mai costruiti.

Aveva un volume di 211 890 m^3 e una massa di 118 000 kg ed era riempito di idrogeno, che ha la densità di 9 * 10^-2 kg/m^3.

La densità dell’aria è 1,29 kg/m^3. 

Quale spinta ascensionale faceva volare l’Hindenburg?

F Archimede = (densità fluido ) * g * (Volume immerso);

FA = d aria * V * g;

FA = 1,29 * 211 890 * 9,81 = 2,681 * 10^6 N;

M = 118 000 kg; (massa dirigibile).

m idrogeno = V * (d idrogeno) = 211 890 * (9 * 10^-2) = 19 070 Kg ; (massa di H)

Fp = (M + m idrogeno) * g = (118 000  + 19 070) * 9,81 = 137 070 * 9,81 =  kg = 1,345 * 10^6 N;

F risultante = FA – Fp; (spinta ascensionale verso l’alto).

Frisultante = 2,681 * 10^6 – 1,345 * 10^6 = 1,336 * 10^6 N = 1,34 * 10^6 N (circa).

LZ 129 Hindenburg era il nome di un dirigibile Zeppelin tedesco. Chiamato così in onore del secondo presidente della Repubblica di Weimar, Paul Von Hindenburg, è stato il più grande oggetto volante mai costruito.

Il 6 maggio 1937 alle 19:25, l’Hindenburg prese fuoco e venne completamente distrutto, nel giro di circa mezzo minuto, mentre cercava di attraccare al pilone di ormeggio della Stazione Aeronavale di Lakehurst (New Jersey).

2) Un tecnico ha massa m = 75 kg e deve salire su un dirigibile con la sua attrezzatura per effettuare misurazioni ad alta quota. Il dirigibile è riempito di elio e ha un volume di 650 m^3. La densità dell’atmosfera è pari a 1,21 kg/m^3 e quella del gas elio è di 0.179 kg/m^3.

– Quanto vale la spinta di Archimede sul dirigibile (trascurare la massa del dirigibile)?

– Determinare per quale valore della massa M dell’attrezzatura la forza peso totale del dirigibile ha la stessa intensità della spinta di Archimede.

F Archimede = d g V = 1,21 * 9,81 * 650 = 7142 N,

Massa Elio = (d elio) * V = 0,179 * 650 = 116,35 kg;

F peso Elio = 116,35 * 9,81 = 1141,4 N; (Peso Gas Elio);

F peso tecnico = 75 * 9,8 = 736 N; (peso uomo);

F peso attrezzatura = M * 9,81;

F peso totale = F Archimede;

1141,4 + 736 + M * 9,81 = 7142;

M * 9,81 = 7142 – 1141,4 – 736;

M = 5264,6 / 9,81 = 537 kg; (massa dell’attrezzatura massima che si può caricare sul dirigibile).

Esercizi di relatività ristretta

1. Un elettrone inizialmente in quiete è sottoposto a una differenza di potenziale Delta V = 5 * 10^5 V : calcolare la sua velocità, utilizzando per l’energia cinetica l’espressione classica e quella relativistica.
   
   

Energia cinetica finale classica:

1/2 m v^2 = e * (DeltaV);

v = radicequadrata( 2 * e * DeltaV/m);

v = radice[(2 * 1,602 * 10^-19 * 5 * 10^5 ) /(9,11 * 10^-31)];

v = radice[1,76 * 10^17] = 4,19 * 10^8 m/s >> c; impossibile.

l’elettrone non può superare la velocità della luce; v < c, sempre,

per il secondo principio della relatività ristretta di Einstein.

Energia finale relativistica:

Ec = [moc^2 / radice(1 – v^2/c^2) ] – moc^2;

mo c^2 = energia a riposo.

e * DeltaV = Ec;

1,602 * 10^-19 * 5 * 10^5 = 8,01 * 10^-14 J; (Lavoro = energia cinetica finale)

moc^2 = (9,11 * 10^-31) * (3 * 10^8)^2 = 8,199 * 10^-14 J; (energia a riposo).

Ec + moc^2 = moc^2 / radice(1 – v^2/c^2);

radice(1 – v^2/c^2) = moc^2 / (Ec + moc^2);

1 – v^2/c^2) =[moc^2 / (Ec + moc^2)]^2;

v^2/c^2 = 1 – [moc^2 / (Ec + moc^2)]^2;

v^2/c^2 = 1 – [8,199 * 10^-14 /( 8,01 * 10^-14 + 8,199 * 10^-14)]^2 ;

v^2 / c^2 = 1 – [8,199 *10^-14 /1,621 * 10^-13]^2;

v^/c^2 = 1 – [0,5058]^2 = 1 – 0,2559;

v^2 = (1 – 0,2559) * c^2;

v = c * radicequadrata(0,744) = c * 0,863;

v = (3 * 10^8) * 0,863;

v = 2,59 * 10^8 m/s; (v elettone; v < c).

Moto di un elettrone in un campo elettrico. In questa situazione l’elettrone viene frenato dal campo in quanto l’elettrone è una particella negativa. Le linee di forza del campo vanno verso il polo negativo, l’elettrone si fermerà e verrà respinto dalle cariche negative.

Esercizio 2

Un collisore è un particolare acceleratore di particelle in cui le particelle accelerate in versi opposti lungo traiettorie circolari vengono fatte collidere frontalmente con velocità uguali e opposte. Supponiamo di considerare un elettrone con velocità 𝑣=𝑥𝑐 (𝑐 indica la velocità della luce nel vuoto) nel sistema di riferimento del laboratorio, che collide frontalmente con un positrone (particella che ha la stessa massa dell’elettrone, ma carica opposta) che ha velocità uguale e opposta a quella dell’elettrone.

Scrivere la funzione che esprime l’energia cinetica relativistica degli elettroni nel sistema di riferimento del laboratorio. Scrivere l’equazione della fisica classica che permette di esprimere la velocità dell’elettrone misurata dal sistema di riferimento del positrone.
Nella teoria della relatività ristretta le trasformazioni di Galileo sono sostituite dalle trasformazioni di Lorentz.

Energia cinetica relativistica:

K = moc^2/[radice(1 – v^2/c^2)] – moc^2;

mo = massa a riposo;

Y = 1 /[radice(1 – v^2/c^2)]  = fattore gamma. 

K = moc^2 *(Y – 1)

Energia cinetica classica = 1/2 mo v^2;

Composizione velocità galileiana:

u’ = u – v;

u’ = u – (-u) = 2u; (velocità dell’elettrone vista dal sistema del positrone).

u’ = xc + xc = 2xc; se x = 0,5 o maggiore di 0,5, allora u’ raggiunge o supera la velocità della luce c; non è possibile.

Composizione relativistica:

u’ = (u – v) /[1 – uv/c^2];

u = xc, (velocità elettrone visto dal laboratorio);

v = – xc; (velocità positrone visto dal laboratorio);

u’ = (velocità elettrone visto dal sistema del positrone).

u’ = (xc + xc) / [1 + x^2c^2/c^2];

u'(x) = 2c x / (1 + x^2); x < 1; (f(x).

se x = 1 abbiamo due particelle a velocità c e questo non è mai verificato per particelle con massa.

Esercizi di calorimetria – Termodinamica – macchine.

Tag

Esercizi di calorimetria e termodinamica, Problemi ambientali - macchine

Lavoro su automobili, mobilità, ambiente, qualità della vita, messaggi ingannevoli su libertà, natura, pressione delle auto sul pianeta di Teodoro Forcellini. Interessante da vedere.

https://drive.google.com/file/d/1CVUL3yrr07fWD4IXhlEmvqLODu

Libertà di viaggiare?

Pubblicità ingannevole?

1. Un blocco di 0,500 kg di grafite si trova alla temperatura di 35,0 °C e riceve energia con una potenza di 10,0 W per 2,00 minuti. Il calore specifico della grafite è 709 J/(kg · K).
   – Calcola la temperatura finale in K del blocco di grafite supponendo che tutta l’energia ricevuta si trasformi in calore.

Energia termica = Q;

Q = c * m * (T – To); (equazione fondamentale della calorimetria).
c = calore specifico; m = massa in kg; T – To = variazione di temperatura.

tempo t = 120 secondi.

Q = P * t = 10,0 * 120 = 1200 J.

T – To = Q / (c * m);

T – To = 1200 / (709 * 0,500) = 3,4°C ( (o Kelvin).

Le differenze di temperatura DeltaT non cambiano se sono in °C o Kelvin.

Temperatura finale:

T = To + 3,4° = 35,0° + 3,4° = 38,4°C .

T in kelvin:

T = 38,4° + 273 = 311,4 K.

2) Un tubo di acciaio con una lunghezza iniziale di 10 m viene riscaldato da 15 °C a 300 °C.
Calcolare l’allungamento del tubo.

L = Lo + Lo * α * ( T – To); legge di dilatazione lineare.

L – Lo = ΔL = Lo * α * ΔT .

Coefficiente di dilatazione termica lineare α dell’acciaio = 12*10^-6 °C^-1;

ΔL = Lo * α * ΔT = 10 * 12 * 10^-6 * 285 = 0,034 m = 34 mm.

3) Un cubo di rame ha lo spigolo di 10 cm, si trova a temperatura di 20°C.

A quale temperatura bisogna portarlo perché il suo volume sia 1012 cm^3 ?

Qual è l’aumento percentuale di volume? (coefficiente di dilatazione lineare del rame α = 1,6 * 10^−5°C^−1).

 

Delta V = Vo * (3 * α) * (DeltaT)

α= 1,6 * 10^−5°C^−1 ,

Vo = 10^3 = 1000 cm^3;

DeltaV = 1012 – 1000 = 12 cm^3;

DeltaT = Delta V / [ Vo * (3 α)];

Delta T = 12 / (1000 * 4,8 * 10^-5) = 250°C;

T – To = 250°

T = 250° + 20° = 270°C;

(DeltaV) / V = 12/1000 = 0,012;

Aumento percentuale = 1,2 %;

12 : 1000 = x : 100;

x = 100 * 12/1000 = 1,2; (aumento %).

4) Ciclo termodinamico.

In un cilindro, dotato di pistone scorrevole, si trova una certa quantità di gas perfetto. Il gas occupa inizialmente un volume di 36 dm3, una pressione di 10^5 Pa e si trova alla temperatura TA =  300 K (stato A). Bloccando il pistone si scalda il gas fino a una temperatura TB =  650 K (stato B). In seguito si lascia espandere il gas mantenendo la temperatura costante fino a che raggiunge un determinato volume (stato C).

Si blocca nuovamente il pistone e si raffredda il gas raggiungendo la pressione iniziale (stato D) alla temperatura TD = 500 K. Si lascia infine libero il pistone e mantenendo costante la pressione lo si riporta allo stato iniziale A.

a. Disegna il grafico p-V del ciclo descritto.

b. Quanto vale la variazione di energia interna del ciclo termodinamico?

Ciclo termodinamico: A —-> B —-> C —-> D —-> A: isocora, isoterma, isocora, isobara.

Stato A: (PA; VA; TA) = (10^5 Pa; 36 dm^3; 300 K).

Da A a B: isovolumica o isocora; VB = VA.

PB / VB = PA / VA; Pb = PA * 650 / 300 = 2,17 * 10^6 Pa

Stato B: (PB; VB; TB) = (2,17 * 10^5 Pa; 36 dm^3; 650 K);

da B a C: isoterma, T costante; TC = TB.

Legge delle isoterme:

PB * VB = PC * VC;

VC = VD; (vedi grafico).

manca VD; lo troviamo con l’ultima isobara da D ad A.

Da D ad A: isobara, P costante.  PD = PA; (si chiude il ciclo).

VD / TD = VA / TA;

VD = 36 * TD / TA = 36 * 500 /300 = 60 dm^3;

Stato D:

(PD; VD; TD) = (10^5 Pa; 60 dm^3; 500 K).

da B a C: isoterma; TC = 650 K

PB * VB = PC * VC;

VC = VD = 60 dm^3;

PC = PB * VB / VC = 2,17 * 10^5 * 36 /60 = 1,3 * 10^5 Pa;

il volume aumenta, la pressione diminuisce.

DeltaU = UA – UA = 0 J; 

L’energia interna è una funzione di stato, dipende dalla temperatura.

La variazione di energia interna dipende dalla variazione di temperatura, se si ritorna in A, T non cambia,

DeltaU = 0 J.

5) Una piscina ha dimensioni: 25 m * 12 m * 1,8 m .

• Calcolare il calore necessario per riscaldarla di 5°C.

• Quanto calore riceve ogni litro d’acqua?

1 litro = 1 dm^3; densità dell’acqua = 1 kg /dm^3 = 1000 kg/m^3.

c = calore specifico = 4186 J/kg°C. (c = 1 kcal/kgK);

Massa totale di acqua: M = densità * Volume.

M = 1000 * (25 * 12 * 1,8) = (1000 kg/m^3) * 540 m^3 = 5,4 * 10^5 kg.

Q = c * M * (Delta t)= 4186 * 5,4 * 10^5 * 5° = 1,13 * 10^10 J.

Q1 = 4186 * 1 * 5° = 20930 J = 2,1 * 10^4 J.

6) A 0.0500 kg ice cube starts at To = -18.5°C.
How much heat does it take to melt it completely?

Q = c * m * (0° – (- 18.5°) + Q fusion.

Qfusion =  3,335 * 10^5 * mass. (Heat of fusion of ice).

Q = 2220 * 0.0500 * (+18.5°) + 3,335 * 10^5 * 0,0500;

Q = 2053.5 + 16675 = 18728.5 J = 1.9 * 10^4 J.

7) Quanti grammi di acqua, a 100 °C, diventano vapore con la stessa quantità di energia che occorre per portare la massa di 1 kg di acqua da To = 0°C fino all’ebollizione pari a T = 100°C?

Q = c * m * (DeltaT);

m = 1 kg; calore specifico dell’acqua c = 4186 J/kg°C;

Delta T = T – To = 100° – 0°.

Q = 4186 * 1 * 100° = 418600 = 4,186 * 10^5 J;

calore di vaporizzazione dell’acqua: cv = 2,260 * 10^6 J/kg;

Q v = cv * m;
m = Q / Cv;

m = 4,186 * 10^5  / 2,260 * 10^6  = 0,2 kg = 200 grammi.

Esercizi su urti. Impulso e quantità di moto.

1) Un carrello avente massa 0,75 kg con misuratore di impulso montato davanti è lanciato con velocità vo = 2 m/s lungo un binario morto, alla fine del quale urta contro un respingente.
Il rilevatore di impulso dopo l’urto segna I = 2,90 Ns

1. qual è la percentuale di energia cinetica persa nell’urto? 

I = m * v – m * vo;

il carrello arriva con velocità vo = + 2 m/s; viene respinto con velocità v di verso contrario.

L’impulso che riceve è in verso contrario:

– 2,9  = 0,75 * v – 0,75 * 2;

0,75 * v = – 2,9 + 1,5;

v = – 1,4 / 0,75 = – 1,87 m/s

E1 = 1/2 m vo^2 = 1/2 * 0,75 * 2^2 = 1,5 J;

E2 = 1/2 m v^2 = 1/2 * 0,75 * (- 1,87)^2 = 1,3 J;

Delta E = 1,3 – 1,5 = – 0,2 J (energia persa).

Impulso di un forza: è il prodotto della forza agente per la durata  Delta t della forza.
I = F * Delta t;

Si chiama quantità di moto di un corpo di massa m,  il prodotto massa * velocità

Q = m * v.

F = m * a;     2° principio della dinamica di Newton.

F = m * (v – vo) / ( Delta t);

F * (Delta t)  = m * v – m * vo.

Teorema dell’impulso:

L’impulso di una forza I che agisce su un corpo di massa m,  è uguale alla variazione della quantità di moto del corpo stesso.

m * v = Q;   si chiama quantità di moto: massa * velocità.

I = (Forza) * (Delta t); si chiama impulso I.

F * (Delta t) = mv2 – m v1;

L’impulso si misura in N s o kg m/s

Pendoli di Newton

2) Una palla di massa, M = 133 g, viene lasciata cadere da un’altezza di 22 m con velocità nulla. Urta il suolo e risale sino all’altezza di 7 m. Se l’urto dura 2 ms; qual è il modulo della forza media esercitata dal suolo sulla palla?

v1 è la velocità con cui arriva a terra, negativa perché verso il basso:
v1 = radquad( 2 * 9,8 * 22) = – 20,77 m/s
v2 è la velocità con cui riparte, positiva, verso l’alto, sarà minore perché arriva a 7 m di altezza:
v2 = radquad(2 * 9,8 * 7) = + 11,71 m/s

Delta t = 2 * 10^-3 s;
F * 2 * 10^-3 = 0,133 * 11,71 – 0,133 * (- 20,77)
F * 2 * 10^-3 = 4,32 Ns
F = 4,32 / (2 * 10^-3 ) = 2160 N circa

3) Una biglia di acciaio di 80 g colpisce con velocità vo =  7,8 m/s un pavimento e rimbalza con una velocità v di modulo 7,8 m/s.

 Calcolare  intensità, direzione e verso dell’impulso che il pavimento ha esercitato sulla biglia.

Impulso I = m * v – m * vo,
L’impulso della forza (I = F * Delta t), è uguale alla variazione della quantità di moto (m v – m vo).
m = 0,080 kg;

vo = – 7,8 m/s; velocità iniziale, la bilia arriva a terra con velocità verso il basso, quindi negativa.

v = + 7,8 m/s; velocità finale, la bilia rimbalza verso l’alto, la velocità cambia verso, quindi diventa positiva.

I = 0,080 * (+ 7,8 ) – 0,080 * (- 7,8) ;

I = 0,080 * ( 7,8 + 7,8) = + 1,25 Ns.

Il pavimento esercita sulla pallina una forza impulsiva verso l’alto; l’impulso I ha direzione verticale, verso l’alto.

Esercizi – Spinta di Archimede in acqua di mare. Pressione. Spinta in atmosfera

Tag

Spinta di Archimede

L’aria è più densa del gas all’interno dei palloncini (Elio He), quindi la Spinta di Archimede che
produce è maggiore della forza peso.

La spinta di Archimede deve  essere almeno uguale al peso dell’anfora in acqua.

F peso fuori dall’acqua = m * g = 95 * 9,8 = 931 N;
Spinta che l’anfora riceve per l’acqua che sposta con il suo volume senza pallone.
Volume in m^3 = 0,038 m^3;

F Archimede = d g V = 1030 * 9,8 * 0,038 = 384 N; (verso l’alto).
F risultante= 931 – 384 = 547 N ( Forza risultante in acqua, peso apparente dell’anfora).
Ci vuole una spinta verso l’alto di 547 N.
F spinta = d g (V pallone):
V pallone = 547 / (1030 * 9,8) = 0,054 m^3 ;
Volume pallone = 54 dm^3 (circa).

2) Un pallone sferico del diametro di 3 m è riempito di elio ( d= 0,00018 g/cm3 = 0,18 kg/m^3). Quanto vale la spinta di Archimede che riceve nell’aria ( d= 0,00129 g/cm^3 = 1,29 kg/m^3) ?

Farchimede = (densità aria) * g * (Volumepallone)

Volume pallone = 4/3 * 3,14 * raggio^3 = 4/3 * 3,14 * 1,5^3 = 14,14 m^3

densità aria = 1,29 kg/m^3

F archimede = 1,29 * 9,8 * 14,14 = 178,7 N

La densità dell’elio non serve per la forza di Archimede. Serve se si vuole trovare la massa del pallone e il suo peso. Se pesa meno dell’aria spostata, il pallone salirà verso l’alto.

Se il pallone deve sollevare una massa di 10 kg (gomma dell’involucro e attrezzatura appesa), riuscirà a sollevarsi?
Massa Elio = d * volume = 0,18 * 14,4 = 2,59 kg;
Massa totale = 10 + 2,59 = 12,59 kg;

Fpeso = 12,59 * 9,8 = 123,4 N; (verso il basso)

F risultante = 178,7 – 123,4 = 55,3 N (verso l’alto).

3) Una sfera cava, con il diametro esterno di 7,2 cm galleggia nell’acqua restando immersa per una frazione pari a 0,8 del suo volume.
Sia ρ sfera= 4,4 g/cm^3 la densità della sfera. Il raggio r della cavità in centimetri misura?

Volume sfera = 4/3 pigreco r^3;

r = 7,2/2 = 3,6 cm; raggio esterno.

Volume sfera = 4/3 * (3,14159) * 3,6^3 = 195,432 cm^3;

V immerso = 0,8 * (V sfera);

V immerso = 0,8 * 195,432 = 156,35 cm^3;

F Archimede = (ρ acqua) * g * V immerso.

La sfera galleggia quindi la Forza di Archimede verso l’alto è uguale alla forza peso verso il basso.

F peso = m * g;

ρ acqua = 1 g / cm^3

(ρ acqua) * g * (V immerso) = m * g;          semplifichiamo g = 9,8 m/s^2,  rimane:

(ρ acqua) *  V immerso  = m; (massa della lamina che forma la sfera cava).

ρ del materiale della sfera = 4,4 g/cm^3; (se non fosse cava, non galleggerebbe in acqua).

m = (1g/cm^3)* 156,35 cm^3 = 156,35 g;

Volume materiale sfera  = m /(ρ sfera) = 156,35 /4,4 = 35,53 cm^3;

(Volume sfera) – (Volume materiale) = Volume cavità interna;

195,432 – 35,53 = 159,9 cm^3;

Volume cavità:

 4/3 * (3,14159) * (r cavità)^3 = 159,9 cm^3;

r cavità = radicecubica[159,9 * 3 / (4 * 3,14159];

r cavità = [38,173] = 3,37 cm ; (circa 3,4 cm); raggio interno della cavità.

Quindi il materiale della sfera è una lamina sottile di spessore:

s = 3,6 – 3,4 =  0,2 cm = 2 mm. 

4) Calcolare il raggio di una sfera di massa m = 700 g in equilibrio in acqua dolce.

Sfera in equilibrio, vuol dire che la spinta di Archimede verso l’alto è uguale alla forza peso verso il basso. (La sfera se è in equilibrio indifferente in acqua, avrà la stessa densità dell’acqua).

(d acqua) * g * Volume immerso = (m sfera)* g;

g = 9,8 m/s^2 si semplifica.

Se usiamo i grammi come unità di massa, possiamo usare la densità dell’acqua in g/cm^3, otterremo il volume della sfera in cm^3.

d acqua = 1000 kg/m^3 = 1 g/cm^3;

1 * Volume immerso = m sfera;

Volume immerso = 700 grammi / 1 g/cm^3 = 700 cm^3;

Volume immerso = volume acqua spostata = volume sfera.

V = 4/3  pigreco * r^3;

r = radicecubica[(V * 3/4) /pigreco];

r = radicecubica[700 * 3/ 3,14 * 4] = radicecubica(167,11);

r = 5,5 cm; raggio della sfera.

5) Un lingotto è composto da una lega di oro (d=1,93*10^4 kg/m^3) e argento (d=1,05*10^4 kg/m^3) e ha la massa di 0,802 kg. Se si immerge il lingotto in acqua distillata, appeso a un dinamometro, il suo peso risulta 7,19 N.

– Quale volume di oro e quale di argento sono contenuti nel lingotto?

F peso = m * g = 0,802 * 9,8 = 7,86 N; (peso del lingotto in aria).

F peso in acqua = 7,19 N;

F Archimede = 7,86 – 7,19 = 0,67 N; (forza di spinta verso l’alto che fa diminuire il peso).

F Archimede = (d acqua) * g * (Volume immerso);

usiamo le densità in kg/dm^3, è più semplice fare i calcoli.

d acqua = 1 kg / dm^3.

Volume = F Archimede/ (d * g) = 0,67 / (1 * 9,8) = 0,0684 dm^3. (Volume lingotto).

V = 68,4 cm^3. (Volume in cm^3)

d oro = 19,3 kg/dm^3 = 19,3 g/cm^3;

d argento = 10,5 kg/dm^3 = 10,5 g/cm^3.

(m argento) + (m oro) = m totale;

m argento = (V Ag) * (d Ag). 

m oro = (V Au) * (d Au);

m totale = 802 grammi.

V Ag + V Au = 68,4 cm^3.

10,5 * (V Ag) + 19,3 * (V Au) = 802;

10,5 * (68,4  – V Au) + 19,3 * (V Au) = 802;

718,2 – 10,5 * (V Au) + 19,3 * (V Au) = 802;

8,8 * (V Au) = 802 – 718,2;

V Au = 83,8 ( 8,8) = 9,52 cm^3; (Volume oro).

V Ag = 68,4 – 9,52 = 58,9 cm^3; (Volume argento).

Noto problema della corona di Gerone, risolto da Archimede.

La corona di Gerone

La storia completa è questa.  Gerone II, tiranno di Siracusa, fece costruire da un valente orafo una corona d’oro, a forma di rami intrecciati, del tipo di quella riprodotta, per porla a decoro di una statua rappresentante un dio o una dea. Tuttavia quando ricevette la bellissima corona ebbe il sospetto che l’orafo potesse aver sostituito, all’interno della corona, l’oro con l’argento. Per questo il Tiranno chiese ad Archimede di determinare se la corona fosse d’oro massiccio oppure se contenesse all’interno il meno pregiato argento. Ma poiché la corona, di pregevole fattura, doveva ornare il capo di una divinità, era essa stessa un oggetto sacro. Quindi il Tiranno pose ad Archimede la condizione che la corona doveva restare integra.

6) Pressione in Newton/m^2.

In un laghetto circolare di 20 m di diametro si è formata una lastra di ghiaccio che riesce a reggere senza rompersi una massa del valore massimo di 205 kg distribuita su una superficie di 1 m^2. Hai una slitta di massa 110 kg.

1) Su quale superficie minima deve poggiare questa slitta per non rompere la lastra di ghiaccio?

2) Quanto vale la massa massima che si potrebbe distribuire in modo uniforme sull’intera superficie del laghetto senza rompere la lastra di ghiaccio?

Risultati: 0,54m^2;   6,4 * 10^4 kg

Pressione P = F / Area = 205 * 9,8 / 1 m^2 = 2009 Pa; pressione che può sostenere la lastra di ghiaccio.

1. Area = F / P = 110 * 9,8 / 2009 = 0,54 m^2 (Superficie minima su cui deve poggiare la slitta).

2. raggio = diametro / 2 = 10 metri.

Area laghetto = 3,14 * r^2 = 3,14 * 10^2 = 314 m^2;

F peso massima = P * Area = 2009 * 314 = 6,31 * 10^5 N;

Massa = F / g = 6,31 * 10^5 / 9,8 = 6,4 * 10^4 kg; ( massa che può sostenere distribuita su tutta la superficie del laghetto).

7) Una sfera rigida di volume V=785 litri e densità 759 kg/m^3 è ancorata al fondo del mare tramite una molla di costante elastica k. La molla è deformata di deltax =22,9 cm rispetto alla posizione di riposo. Si calcoli la costante elastica della molla.

La sfera è soggetta alla forza peso verso il basso e alla spinta di Archimede che la spinge verso l’alto.

La forza della molla F = k * x verso il basso tiene ferma la sfera sul fondo.

F peso = m * g;

massa m = d * V;

1 litro = 1 dm^3.

Volume: V = 785 dm^3 = 0,785 m^3

m = 759 * 0,785 = 595,8 kg;

F peso = 595,8 * 9,8 = 5839 N;

F Archimede = (d acqua mare) * V * g = 1030 * 0,785 * 9,8 = 7924 N;

d acqua di mare = 1030 kg/m^3 (circa, dipende dalla quantità di sale).

La forza di Archimede è maggiore della forza peso, quindi la sfera salirebbe verso l’alto se non fosse ancorata.

F Archimede – F peso: F  = 7924 – 5839 = 2085 N. (Forza verso l’alto).

La molla deve esercitare una forza uguale e contraria ad F per tenere ferma la sfera.

delta x = 22,9 cm = 0,229 m.

F = k * (delta x);

k = F / (delta x) = 2085 / 0,229 = 9105 N / m; (costante elastica della molla).

k = 9105 N/m in acqua di mare salata.

k = 8100 N/m (circa se fosse in acqua non salata con densità 1000 kg/m^3; la spinta di Archimede verso l’alto sarebbe minore F Archimede = 1000 * 9,8 * V immerso = 7693 N ).

7) Un bicchiere a forma cilindrica con il diametro interno lungo 4 cm contiene acqua. Per raffreddarla sono stati aggiunti 5 cubetti di ghiaccio uguali e il livello dell’acqua si è alzato di 3 cm.

Quanto misurava lo spigolo di ogni cubetto di ghiaccio?

Volume cubetti = Volume acqua spostata nel bicchiere.

Volume immerso dei cubetti = Area base * h = r^2 *3,14 * h;

raggio = 2 cm. h = 3 cm.

I cubetti galleggiano in acqua con la parte immersa che è il 92% del totale perché il ghiaccio ha densità 0,92 g/cm^3.

Forza peso = F Archimede;

V totale * (d ghiaccio) * g = V immerso * (d acqua) * g;

Volume totale = (d acqua / d ghiaccio )* V immerso;

Volume immerso dei cubetti = 2^2 * 3,14 * 3= 12,57 * 3 = 37,7 cm^3;

Volume immerso di 1 cubetto = 37,7/5 = 7,54 cm^3.

densità ghiaccio = 0,92 g/cm^3;

densità acqua = 1 g/cm^3.

Volume totale di 1 cubetto = (d acqua / d ghiaccio )* V immerso ;

Volume totale = 1 / 0,92 * 7,54 = 8,2 cm^3

Spigolo = radicecubica(8,2) = 2,02 cm.

 

Campo magnetico di un solenoide.

Tag

Campo magnetico solenoide

1. Un solenoide è lungo L = 20,0 cm e ha un diametro di 50,0 mm. Il filo di rame per realizzare le spire dell’avvolgimento ha una sezione di diametro di 0,50 mm. Le spire sono affiancate senza spazi fra esse.
   Ai capi del solenoide è applicata una differenza di potenziale V affinché il campo magnetico B al centro del solenoide abbia un’intensità
   B = 1,26 * 10^-3 T.
   La resistività del rame rCu = 1,7 * 10^-8 Ohm m.
   – Calcolare il valore della differenza di potenziale V.

B = mo * N * i / L;

N = numero di spire;

L = 20,0 cm = 200 mm.

diametro filo di rame = 0,50 mm;

le spire sono tutte affiancate, senza spazio fra esse.

N = L / diametro filo = 200 / 0,50 = 400 spire;

mo = 4 pigreco *10^-7 N/A^2 = 1,26 * 10^-6 N/A^2. (Permeabilità magnetica).

B = 1,26 * 10^-3 T;

L = 0,200 m;

i = B * L / (mo * N);

i  = 1,26 * 10^-3 * 0,200 /(1,26 * 10^-6 * 400);

i = 0,5 A (intensità di corrente).

V = R * i;

R = r * (lunghezza filo) / (Area filo); (Resistenza filo di rame).

Diametro spira = 50 mm = 5 cm = 0,05 m.

Lunghezza di una spira = 2 * 3,14 * raggio =

= diametro * 3,14;

Lunghezza di una spira = 0,05  * 3,14 = 0,157 m

Lunghezza filo di rame = N * 0,157;

Lunghezza filo di rame= 400 * 0,157 = 62,8 m;

diametro filo = 0,5 mm = 0,5 * 10^-3 m; 

raggio = 0,25 * 10^-3 m

Area sezione filo di rame = 3,14 * r^2;

Area = 3,14 * (0,25 * 10^-3)^2 = 1,96 * 10^-7 m^2;

Resistenza filo di rame: 

R = r * (lunghezza filo) / (Area filo); 2a legge di Ohm.

R = 1,7 * 10^-8 * 62,8 / (1,96 * 10^-7) = 5,44 Ohm.

V = R * i = 5,44 * 0,5 = 2,7 V.

Esercizi di termodinamica- cicli. Legge di Mayer

1. Un gas biatomico compie un ciclo termodinamico costituito da tre trasformazioni reversibili:

AB isoterma ,

BC isocora,

CA adiabatica . (vedi figura).

Sapendo che VB = 3 VA, sapendo che il calore specifico di un gas biatomico è : cv = 5/2 R; cp = 7/2 R

calcolare il rendimento η del ciclo termodinamico.

Vb = 3 Va;

Lavoro isoterma: (Ta costante),

LAB = n R Ta ln(3 Va / Va) = n R Ta ln(3).

Gas biatomico cv = 5/2 R; cp = 7/2 R;

gamma = cp/cv = 7/5.

Adiabatica Pc * Vc^gamma = Pa * Va^gamma.

Vc = Vb = 3 Va;

Pb = 1/3 Pa;

Pc = Pa * (Va/Vc)^gamma;

Pc = Pa * (1/3)^(7/5);

Pc = Pa * 0,215

isocora:

Pb/Tb = Pc/Tc;

Tb = Ta;

Tc = Pc * Ta / Pb ;

Tc = 0,215 * Pa * Ta / (1/3 Pa) = 0,215 * 3 = 0,645 * Ta.

Lavoro adiabatica = – cv n (Ta – Tc) = 

= – 5/2 R n (Ta – 0,645 Ta) = – 5/2 R n Ta * 0,355;

rendimento η = L / Qassorbito.

Q assorbito solo nell’isoterma da A a B.

η = [n R Ta ln(3) – 5/2 R n Ta * 0,355] / n R Ta ln(3) ;

n R Ta si semplifica, resta:

η = [ln(3) – 5/2 * 0,355] / ln(3) = (1,1 – 0,89) / 1,1;

η = 0,21 / 1,1 = 0,19 = 19%.

Trasformazioni termodinamiche:

Trasformazione isoterma: P1 V1 = P2 V2; Q = L = n R T ln(V2/V1)

Adiabatica: Q = 0 J. P1 * V1^gamma = P2 * V2^gamma; L = – DeltaU = – cv n DeltaT.

Isocora: L = 0 J ; P1/T1 = P2/T2. L = DeltaU = cv n DeltaT.

ISOBARA – Legge di Mayer

Isobara: P = costate. Q = L + DeltaU = P * DeltaV + cv n DeltaT.

Lavoro nell’isobara per un gas monoatomico cv = 3/2 R J/Kmol:

P * DeltaV = n R DeltaT; per la legge dei gas perfetti.

Q = L + DeltaU = n R DeltaT + cv n DeltaT;
Q = n R DeltaT + 3/2 R n DeltaT;

R + 3/2 R = 5/2 R = cp calore specifico a pressione costante.

cp = cv + R; Legge di Mayer.

Q = cp * n * DeltaT.

2) Una macchina termica ha un rendimento che vale 8,4 %, pari al 72 % di quello di una macchina di Carnot che opera tra le stesse temperature, la cui differenza è di 35°C.

> calcolare le temperature delle due sorgenti ;

> calcolare il coefficiente di prestazione di un frigorifero che operi invertendo il ciclo della macchina termica ideale di Carnot.

0,72 * (r Carnot) = 0,084;

r Carnot = 0,084 / 0,72 = 0,12 (rendimento macchina di Carnot).

T2 – T1 = 35°C; una differenza di 35°C rimane 35 K anche in Kelvin perché le due scale sono centigrade.

(T2 – T1) / T2 = 0,12

35 / T2 = 0,12;

T2 = 35 / 0,12 = 292 K; (circa = 2,9 * 10^2 K)

T2 – T1 = 35;

T1 = 292 – 35 = 257 K; ( circa = 2,6 * 10^2 K).

Il coefficiente di prestazione è l’inverso del rendimento.

cop = T1 / (T2 – T1) = 257 / 35 = 7,3.

Ciclo di Carnot: due isoterme + due adiabatiche; massimo rendimento che dipende dalle due temperature in gioco: rendimento = (T2 – T1) / T2

3) Un recipiente cilindrico contiene 11 * 10^23 atomi di neon.
Il gas si espande isotermicamente alla temperatura di 350 K fino a raggiungere un volume pari al doppio di quello iniziale. Successivamente viene riscaldato di 20°C mantenendo la pressione costante di 1,1 atm.

– Calcolare il lavoro svolto durante tutta la trasformazione.

– Calcolare la variazione di energia interna totale.

– Calcolare il calore totale assorbito o ceduto.

Isoterma AB + isobara BC.

gas neon, è un gas raro.

  MM = 20,18 grammi (ha 10 protoni  e 10 neutroni, totale 20 particelle pesanti).

N = 11* 10^23 atomi;

numero di moli: 

n = N / (N avogadro) = 11 * 10^23 / 6,022 * 10^23;

n = 1,83 moli di gas neon, il gas è monoatomico.

R = 8,31 J/molK;

cv = 3/2 * R J/molK; cp = 5/2 * R J/molK;

Isoterma AB:  Q = L = n R T ln(V2/V1);

V2 = 2 V1;  V2 / V1 = 2;

L AB = 1,83 * 8,31 * 350 * ln(2) = 3689 J = 3,7 kJ.

P = 1,1 atm = 1,1 * 1,013 * 10^5 Pa = 1,114 * 10^5 Pa;

TB = 350 K

L’aumento di DeltaT = 20°C è lo stesso anche in Kelvin.

TC = 350 K +DeltaT = 370 K;

Q isobara = L + DeltaU = P * DeltaV + cv n DeltaT;

P * DeltaV = n R DeltaT 

Lavoro isobara = n R (Tfin – To) =1,83 * 8,31 * (370 – 350);

L isobara = 304,15 J = 0,304 kJ;

Lavoro = 3,7 + 0,304 = 4,0 kJ; (lavoro totale).

DeltaU isoterma = 0 J perché non aumenta la temperatura.

DeltaU Isobara = cv n DeltaT = 3/2 * 8,31 * 20 = 249 J;

Q isobara = L + DeltaU = 304 + 249 = 553 J;

Q isoterma = L = 3689 J;

Q assorbito = Q isoterma + Q isobara,

Q ass = 3689 + 553 = 4242 J = 4,24 kJ. 

Esercizi sul moto rettilineo, moto di un grave lanciato verso l’alto.

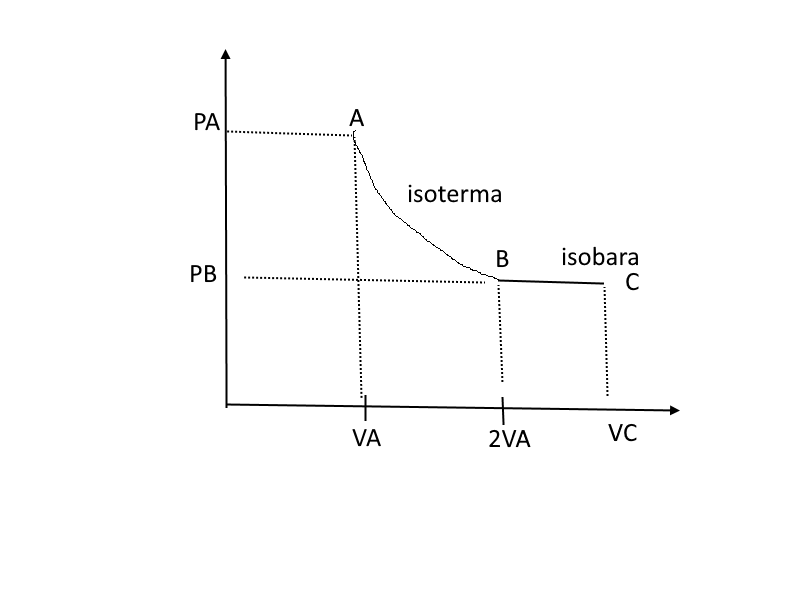
Legge del moto rettilineo uniforme: v = costante.

S = v * (t – to) * So.

Legge del moto uniformemente accelerato:

v = a * (t – to) + vo;   (legge della velocità).

a = (v – vo) / (t – to);  (accelerazione).

S = 1/2 a t^2 + vo * t * So;   (legge dello spazio percorso).

Esempio 1: Esercizio moto uniforme e moto accelerato.

Un’ auto da corsa effettua un pit stop. Riparte da ferma e lascia l’area del pit stop con un’accelerazione di 6,0 m/s^2, impiegando 6,0 s per entrare nel circuito. Nello stesso istante di entrata nel circuito, una seconda auto la affianca ad un velocità di 60 m/s e la supera. La prima auto mantiene la stessa accelerazione.
Dopo quanto tempo la prima auto raggiunge la seconda?

Velocità raggiunta in 6,0 s:

v = a * t;

v = 6,0 * 6,0 = 36 m/s; (velocità con cui entra nel circuito).

Continua ad accelerare:

S = 1/2 a t^2 + vo t;

S = 1/2 * 6,0 * t^2 + 36 * t; legge sel moto.

Seconda auto: viaggia a velocità costante.

S = 60 * t;

Mettiamo a sistema le due leggi del moto.

S = 3,0 t^2 + 36 t;    (1).

S = 60 t;  (2).

Eguagliamo S = S; troviamo il tempo in cui la prima auto raggiunge la seconda.

 3,0 t^2 + 36 t = 60 t;

3,0 t^2 – 24 t = 0;

t * (3,0 t – 24) = 0;

t1 = 0; situazione iniziale.

t2 = 24 / 3,0 = 8 s;

la prima auto raggiunge la seconda in 8 secondi.

Esempio 2:

L’auto B parte con un vantaggio di 200 m e 35,0 s prima dell’auto A.
A si muove alla velocità di 30,0 m/s e B alla velocità 25,0 m/s.

1) qual è il vantaggio di B nell’istante in cui parte A?

2) Dopo quanti secondi dalla sua partenza A raggiunge B?

3) Quale velocità avrebbe dovuto avere A per raggiungere B in soli 200 s dall’istante della sua partenza?

Legge del moto:

S = v * t + So

Sa = 30,0 * t;

L’auto A parte a t = 0 s, quando l’auto B è già partita 35 secondi prima.

Sb = 25 * (t + 35,0) + 200;

Sb = 25,0 * t + 875 + 200;

Sb = 25,0 * t + 1075;

1)  So = 1075 m; vantaggio di B su A.

2)  Sa = Sb;  A raggiunge B;

30,0 * t = 25,0 * t + 1075;

5,0 t = 1075

t = 1075 / 5 = 215 s;  A raggiuge B in 215 s.

3) t = 200 s; velocità di A:

va * 200 = 25,0 * 200 + 1075

va * 200 = 6075;

va = 6075 / 200 = 30,375 m/s;   va = circa 30,4 m/s.

Berlino, oro e record del mondo nei 100 m per Usain Bolt: 9″58.

Il precedente primato Bolt lo aveva ottenuto alle Olimpiadi di Pechino del 2008 correndo in 9,69 s. Argento per l’americano Tyson Gay in 9,71 s, bronzo per l’altro giamaicano Asafa Powell in 9,84 s

finale dei 100 m a Berlino – 16 agosto 2009.

L’accelerazione è la variazione di velocità nell’unità di tempo:

a = (v-vo) / (t – to)     si misura in m/s^2.

Il 16 agosto 2009 a Berlino, Bolt ha corso i 100 m in un tempo t = 9,58 s, record del mondo.

1) Calcolare la velocità media in m/s e in km/h. 

v media = s/t = 100 / 9,58 = 10,44 m/s.

  ( Ris :  10,44 m/s; 37,58 km/h).

Ma Bolt ha raggiunto una velocità finale molto maggiore.

Supponendo che Bolt abbia mantenuto un moto accelerato per un tempo t1 = 4 s e che  il suo moto sia stato uniforme per il rimanente tempo t2 = 5,58 s,

• calcolare l’accelerazione a,
• lo spazio S1 di accelerazione,
• la velocità raggiunta alla fine della fase di accelerazione,
• lo spazio S2 percorso con tale velocità.

Ris :  ( a =3,3 m/s^2; S1 =26,4 m; V = 13,2 m/s = 47,5 km/h: S2 = 73,7 m).

Impostare il seguente sistema: 

S1 = 1/2  a  t1^2   ;                S1 = 1/2 * a * 4^2 = 8 * a;

S2 = V * t2                               S2 = 5,58 * v

v = a * t1                                 V = 4 * a

S1 + S2 = 100                          

Soluzione:

S1 = 1/2 a t1^2; (moto accelerato).

S1 = 1/2 a * 4^2;

S1 = 1/2 * a * 16 ;S1 = 8 * a;

S2 = v * t2; (moto uniforme).

S2 = 5,58 * v ;

v = a * t1 ;

v = a *4, (velocità raggiunta nei primi 4 secondi).

S2 = 5,58 * a * 4 = 22,32 * a;

S1 + S2 = 100;

8 * a + 22,32 * a = 100;

30,32 * a = 100;

a = 100 / 30,32 = 3,3 m/s^2;

v = a * t1 = 3,3 * 4 = 13,2 m/s; (velocità raggiunta);

in km/h: v =  13,2 m/s = 13,2 * 3,6 = 47,52 km/h.

S1 = 8 * 3,3 = 26,4 m;

S2 = 100 – 26,4 = 73,6 m.

Esercizio 1

vo = 0 m/s;

v = 97,2 km/h = 97200 m / 3600 s = 97,2 / 3,6 = 27 m/s;

a = (v – vo) / t = 27/9,00 = 3 m/s^2; accelerazione.

v = 3 * t, con t da 0 s a 9,00 s.

S = 1/2 a t^2 = 1/2 * 3 * 9^2 = 121,5 m; (Spazio percorso).

Poi moto uniforme, con v = 27 m/s:

S = v * t;

t = S / v = 297 /27 = 11,00 s. (Tempo di moto uniforme).

ultimo tratto decelera: a = – 1,5 m/s^2; v finale = 0.

v = a * t + vo;

v = – 1,5 * t + 27;

– 1,5 * t + 27 = 0;

t = 27/1,5 = 18,00 secondi; (tempo per fermarsi).

S = 1/2 * (- 1,5) * 18^2 + 27 * 18 = 243 m; (spazio di frenata).

Tempo totale = 9,00 + 11,00 + 18,00 = 38,00 s.

S totale = 121,5 + 297 + 243 = 661,5 m.

Grafico del moto: velocità – tempo.

Lo spazio percorso in metri è dato anche dall’area sotto il grafico, (area del trapezio):

S = (38 + 11) * 27 / 2 = 661,5 m.

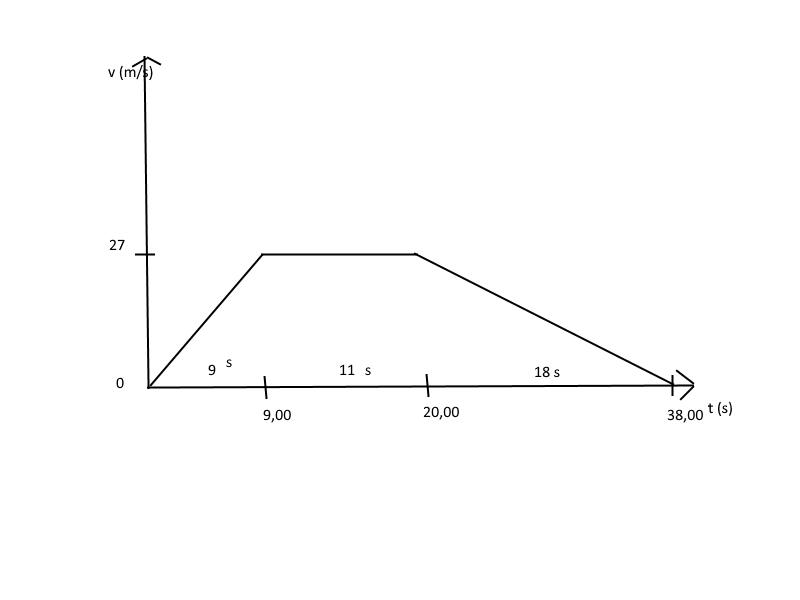
Esercizio 2

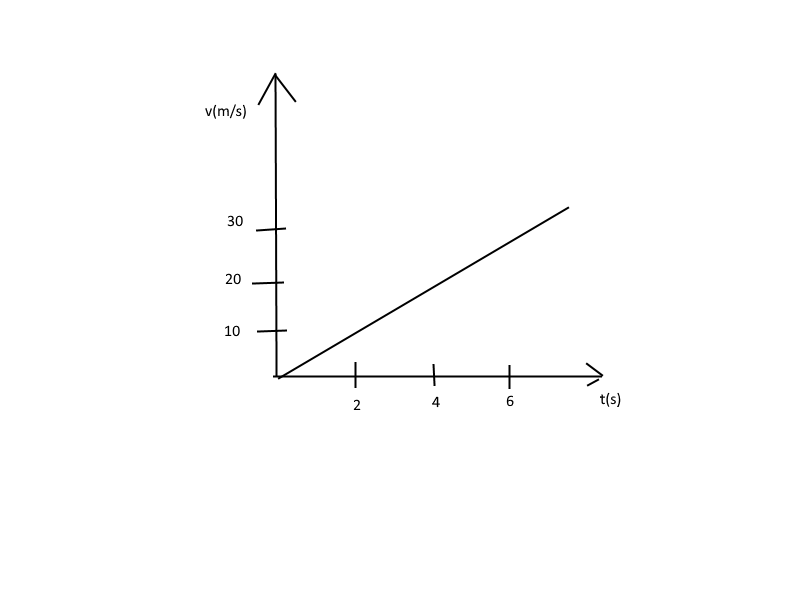
Scrivere la legge della velocità per il moto rappresentato dal grafico in figura.

– Calcolare la distanza percorsa nell’intervallo di tempo fra 1,0 s e 2,0 s.

Soluzione= 20 m

La velocità aumenta nel tempo, c’è accelerazione costante.

vo = 5 m/s;      v finale: v = 25 m/s.

a = (v – vo) / (t – to) = (25 – 5) / (2,0 – 0);

a = 20/2,0 = 10 m/s^2;

v = 10 * t  + 5;  legge del moto per la velocità.

Lo spazio lo si può calcolare come area sotto il grafico della velocità. E’ l’area di un trapezio: le basi sono le velocità, l’altezza è il tempo.

v1= 10 * 1 + 5 = 15 m/s;

v2 = 10 * 2 + 5 = 25 m/s; come si legge dal grafico.

S = (v1 + v2) * (t2 – t1) / 2 = (15 + 25) * 1,0 / 2 = 20 m.

Oppure con la legge del moto dello spazio:

S = 1/2 a (t- to)^2 + vo * (t – to).

vo  al tempo 1,0 s = 15 m/s;

S = 1/2 * 10 * (2,0 – 1,0)^2 + 15 * 1,0 = 5 * 1,0 + 15 = 20 m.

Esercizio 3

La legge oraria di una persona che si sta muovendo in bicicletta è:

x= 6,0 m + (4,5 m/s) * t.

a. Dove si trova la bicicletta al tempo  t = 2,0 s?

b. Per quale valore del tempo t, la bicicletta si trova in x = 24 m?

x = xo + v * t ; legge del moto.

a) t = 2,0 s:

x = 6,0 + 4,5 * 2,0 = 6,0 + 9,0 = 15 m; posizione della bici.

b) x = 24 m; trovare il tempo t.

6,0 + 4,5 * t = 24;

4,5 * t = 24 – 6,0;

4,5 * t = 18;

t = 18 / 4,5 = 4,0 secondi.  ( Dopo 4 secondi la bici ha percorso 18 metri, aggiungendo i 6,0 m della posizione iniziale, la bici si troverà a 24 m).

Esercizio 4

Quanto è lungo un treno (dalla motrice fino all’ultimo vagone) se attraversa completamente  un ponte lungo 200 m in 13,0 s, ad una velocità costante di 80,0 km/h?

v = 80 km/h = 80000/ 3600 = 80/3,6 = 22,22 m/s;

S =v * t;

In t = 13,0 s; il treno percorre tutto il ponte, + tutta la sua lunghezza L;

v * t = L + 200.

22,2 * 13,0 = L + 200;

288,6 = L + 200;

L = 288,6 – 200 = 88,6 m, lunghezza del treno.

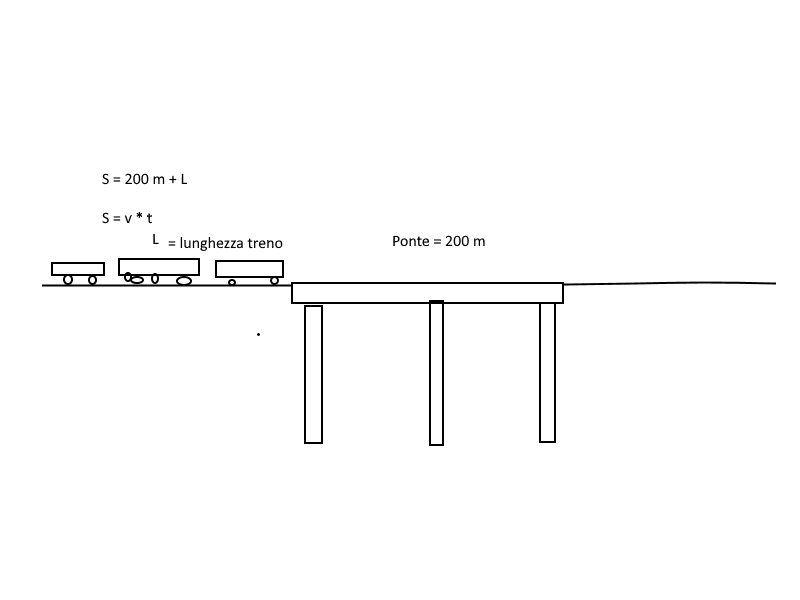
Esercizio 5 – quattro semplici esempi a), b), c), d):

a) Un’auto accelera costantemente per 10 s con accelerazione a uguale a 4 m/s^2 . Sapendo che la sua velocità iniziale è vo = 6 m/s determinare la sua velocità finale.

v = a * t + vo;

v = 4 * 10 + 6 = 46 m/s.

b) Un’auto viaggia a una velocità di 144 km/h. Quanto tempo impiega a fermarsi se i freni forniscono una decelerazione costante di 5 m/s^2 . Quanto spazio percorre prima di fermarsi?

vo = 144 km/h = 144 000 m/3600 s = 40 m/s;

v = – 5 * t + 40;

v = 0 m/s; velocità finale.

– 5 * t + 40 = 0

t = – 40 / (-5) = 8 s; tempo per fermarsi.

Legge del moto:  S = 1/2 a * t^2 + vo t;

S = 1/2 * (-5) * 8^2 + 40 * 8 = 160 m.

c) Un’auto si muove di moto rettilineo uniformemente accelerato con accelerazione uguale a a = 5 m/s^2 . Sapendo che la sua velocità iniziale è vo = 10 m/s, qual è la sua velocità dopo 3 s ?

v = 5 * 3 + 10 = 25 m/s.

d) Un’automobile parte da ferma con accelerazione costante uguale a 5 m/s^2 .

a) Calcolare la velocità raggiunta dopo 4 s.

b) Calcolare quanto tempo è necessario per raggiungere la velocità di 108 km/h

c) Rappresentare con un diagramma velocità-tempo il moto dell’auto.

v = a * t = 5 * 4 = 20 m/s;

v finale = 108 km/h = 108 000 m / 3600 s = 108 / 3,6 = 30 m/s.

v = a * t;

t = v / a = 30 / 5 = 6 secondi.

5) vo = 288 km/h = 288 / 3,6 = 80 m/s;

v finale  = 0; t = 4 secondi.

a * t + 80 = 0;

a = – 80 / 4 = – 20 m/s^2.

Esercizio 6:

Una particella in moto lungo l’asse delle x si muove con accelerazione costante da x = 2,0 m a x = 8,0 m in un intervallo di 2,5 s.
La velocità della particella a x = 8,0 m è 2,8 m/s.

• Qual è l’accelerazione durante l’intervallo considerato?
• Qual è la velocità iniziale?

x = 1/2 a t^2 + vo * t + xo;  (legge del moto accelerato).

xo = 2,0 m;

v = a * t + vo;   (legge del moto accelerato per la velocità).

v = 2,8 m/s;

t = 2,5 s;

vo = v – a * t;

vo = 2,8 – a * t;

8,0 = 1/2 * a * 2,5^2 + (2,8 – a * 2,5) * 2,5 + 2,0;

8,0 – 2,0 = 3,125 * a + 7,0 – 6,25 * a;

6,0 – 7,0 = – 3,125 * a;

a = – 1 / (- 3,125) = 0,32 m/s^2; accelerazione).

vo = 2,8 – 0,32 * 2,5 = 2,0 m/s; (velocità iniziale).

Esercizio 7:

v = g * t + vo ;

g = – 9,8 m/s^2; (accelerazione di gravità rivolta verso il basso).

– Tempo di salita: è il tempo per raggiungere la quota massima; si pone v = 0 e si ricava t:

g t + vo  = 0

t(salita) = – vo  / g =  -15,00 / – 9,8 = 1,53 s;

– altezza massima:

y = 1/2 g t^2 + v * t; (moto accelerato);

y max = 1/2 * (-9,8) * 1,53^2 + 15 * 1,53 = 11,5 m;

– Tempi a 8 metri.

– 4,9 * t^2 + 15,00 * t = 8;

4,9 t^2 – 15,00*t  + 8 = 0;

t = [15 +- radice(15^2 – 4 * 4,9 * 8) ] /(2 * 4,9) ;t = [15 +-radice(68,2)]/9,8 = [15 +- 8,26]/ 9,8;

Due soluzioni perché l’oggetto passa due volte all’altezza di 30 m, (in salita e in discesa).

t1 = (15 – 8,26) / 9,8 = 6,74/9,8 = 0,69 s; (in salita).

t2 = (15 + 8,26) / 9,8 = 23,26/9,8 = 2,37 s (in discesa).

Tempo di volo. Si pone  y = 0 m.

1/2 g t^2 + v * t = 0;

1/2 * (-9,8) * t^2 + 15,00 * t = 0;

4,9 t^2 – 15,00 t = 0

t * ( 4,9 t – 15,00) = 0

t1 = 0 s; (alla partenza).

t2 = 15,00 / 4,9 = 3,06 s; (al ritorno; t volo = 2 * t salita).

v finale = – 9,8 *  3,06 + 15,00 = – 30,00 + 15,00 = – 15,00 m/s.

Torna a terra con la stessa velocità di partenza cambiata di segno, cioè rivolta verso il basso.

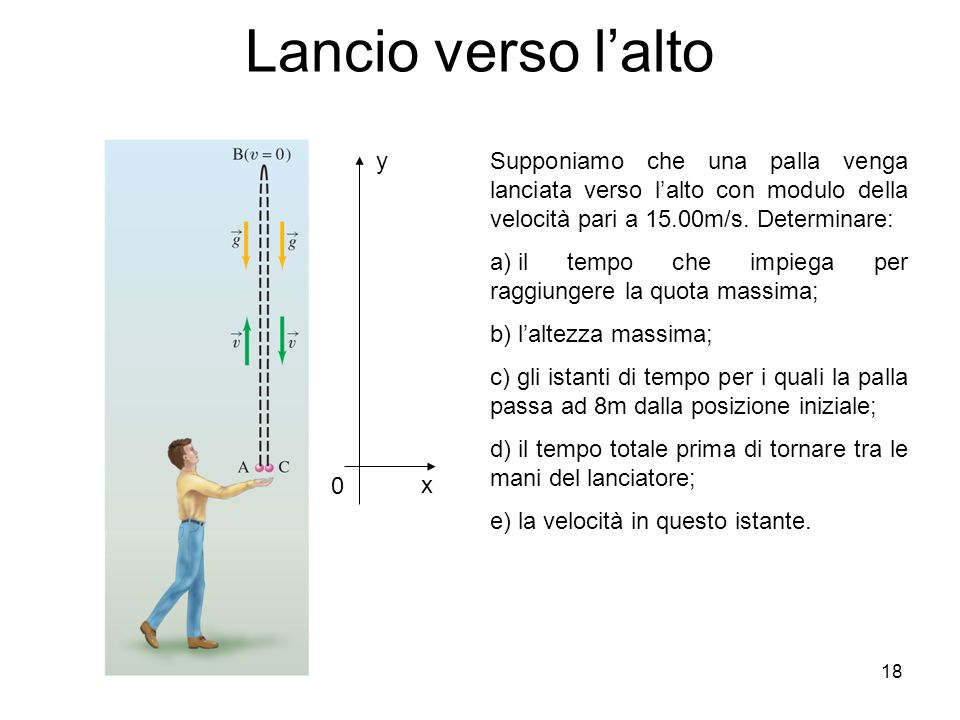
Esercizio 8 :

Un oggetto viene lanciato verticalmente verso l’ alto con una velocità iniziale          vo = 90 km/h.

Determinare i due istanti in cui si trova ad un’altezza di 30 m dal suolo e qual è la velocità dell’oggetto in tali istanti. 

vo = 90 000 m / 3600 s = 90 / 3,6 = 25 m/s; (velocità iniziale).

h = 30 m;

1/2 * (- 9,8) * t^2 + 25 * t = 30.

Troviamo il tempo t:

– 4,9 * t^2 + 25 * t – 30 = 0

4,9 t^2 – 25 t + 30 = 0

t = [25 +- radice(25^2 – 4 * 4,9 * 30) ] /(2 * 4,9) ;

t = [25 +-radice(37)]/9,8 = [25 +- 6,08]/ 9,8;

Due soluzioni perché l’oggetto passa due volte all’altezza di 30 m, (in salita e in discesa).

t1 = (25 – 6,08) / 9,8 = 18,92/9,8 = 1,93 s;

(quando è in salita);

Ripassa a 30 m in discesa:

t2 = (25 + 6,08) / 9,8 = 3,17 s.

v1 = – 9,8 * 1,93 + 25 = + 6,1 m/s, (quando sale).

v2 = – 9,8 * 3,17 + 25 = – 6,1 m/s, (quando scende, stessa velocità però verso il basso).

Esercizio 9:

Un oggetto, lanciato verticalmente verso l’alto, ha una velocità di 18 m/s, quando raggiunge un quarto della sua massima altezza al di sopra del punto di lancio.

• Qual è la velocità iniziale (di lancio) dell’oggetto?

  Applichiamo la conservazione dell’energia :

  m *g * hmax = 1/2 m vo^2;

  h max = vo^2/(2g);

  l’energia è la stessa in ogni punto.

  m * g * h max = m* g* (hmax/4) + 1/2 * m * 18^2

  la massa m si semplifica;

  g *  vo^2/(2g) = g * vo^2/(8g) + 1/2 18^2

  vo^2 / 2 – vo^2/8 = 162

  3/8 vo^2 = 162

  vo = radice(162*8/3) = radice(432) = 20,8 m/s.

Esercizio 10:

Ponte di Augusto e Tiberio a Rimini.

Sei su un ponte che si trova a 15 m sopra un fiume e lasci cadere una pietra. Quando ha percorso una distanza di 3,20 m lanci una seconda pietra. Che velocità deve avere la seconda pietra perché entrambe entrino in acqua nello stesso istante di tempo?

Tempo di caduta da 15 m:

h = 1/2 g t^2;

t = radice(2 h/g) = radice(2 * 15 / 9,8) = 1,75 s;

tempo per percorrere 3,30 m:

t1 = radice(2 * 3,20 /9,8) = 0,808 s;

Dopo 0,808 s lanci la seconda pietra con velocità vo.

La seconda pietra deve percorrere 15 metri e  arrivare al suolo in un tempo:

t2 = 1,75 – 0,808 = 0,94 s;

h = 1/2 g t^2 + vo t;

15 = 1/2 * 9,8 * 0,94^2 + vo * 0,94;

15 = 4,33 + vo * 0,94

vo = (15 – 4,33) / 0,94;

vo = 10,67 / 0,94 = 11,3 m/s.

Esercizio 11:

Una biglia di massa 0,5 Kg viene lasciata libera di cadere da una discesa di altezza incognita. Sapendo che la biglia alla fine della discesa raggiunge una velocità di 1,5 m/s, determinare l’altezza della discesa.

La biglia parte da ferma, poi accelera per l’accelerazione di gravità g = 9,8 m/s^2.

Con la conservazione dell’energia:

Energia potenziale iniziale = Energia cinetica finale.

m g h = 1/2 m v^2;

h = v^2/(2 * g) = 1,5^2 / (2 * 9,8) = 0,11 m = 11 cm.

m g h è l’energia potenziale.

1/2 m v^2 è l’energia cinetica.

Se non si conosce la conservazione, allora utilizziamo le leggi del moto accelerato:

v = g * t;

v = 9,8 * t;

t = v / 9,8 = 1,5/9,8 = 0,153 s ( tempo di caduta)

h = 1/2 * g * t^2; 

h = 1/2 * 9,8 * 0,153^2 = 0,11 m.